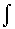Using Waveform Similarity to Constrain Earthquake Locations

William Menke, Lamont-Doherty Earth Observatory, Palisades NY 10964 USA
in press in BSSA, 24 April 1999
(this document is http://doherty.ldeo.columbia.edu/users/menke/eqloc/index.html)
(PostScript version)

Abstract. We demonstrate that the numerical value of the cross-correlation between P or S waveforms, commonly computed to determine differential traveltimes for earthquake relocation, itself contains useful information about the relative location of the events. This information can be used to supplement traditional traveltime inversions (especially when few stations are available) and to investigate the heterogenity that underlies the multiple scattering process.

Introduction

Recently, earthquake relocation techniques have been markedly improved by using very precise differential traveltimes derived by waveform cross-correlation techniques (Got et al. 1994; Nadeau et al., 1995; Slunga et al., 1996; Phillips et al., 1997). This method relies on the similarity of the waveforms of neighboring events, which often match 'wiggle for wiggle'. Differential traveltimes can often be measured to millisecond precision, allowing relative location precise to a few meters.

Differential traveltimes, t_ij, from pairs i and j of a set of N events observed on a common station are estimated from the P (or S) seismograms, u_i and u_j as:

C_ij(t_ij) = max_t c_ij(t)

where c_ij(t) = a_i^-1 a_j^-1 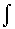u_i(t') u_j(t'-t) dt'

and a_i² = 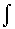u_i²(t') dt'

Here c_ij is the normalized cross-correlation between P (or S) wave seismograms, u_i and u_j. Its maximum values, which can be arranged into a symmetric matrix of correlation coefficients, [C]_ij=C_ij, decreases from unity (when the two seismograms are identical) to near-zero (when they are very different).

Little attention has been paid to the actual value of the correlation coefficients, except that they have sometimes been used to reject traveltime estimates when their value falls below some threshhold (e.g. reject t_ij if C_ij<0.45, Shearer (1998)). Nevertheless, the very idea that neighboring events have similar waveforms (i.e. large C_ij) and more widely separated events have more dissimilar waveforms (i.e. near-zero C_ij) suggests that C contains information on the relative location of a group of events. Such a relationship can be justified by assuming that the waveform dissimilarity arises through multiple scattering interactions that take place between source and receiver. Array studies have indicated that this scattering causes the correlation coefficient - on average - to decline exponentially with the distance, r_ij=|r_ij|, separating the two events: C_ij = exp( -r_ij/s ). Here s is a frequency-dependent correlation length that is typically on the order of one wavelength (Menke et al., 1990; Menke et al., 1991; Nadeau et al. 1995, their figure 2). This behavior has been found to be independent of the viewing angle (that is the angle between r and the ray connecting event and observer) (Menke et al., 1990). The correlation data are in this sense complementary to traveltime data, which only depends on the component of r in the ray direction.

In principle, if C_ij were exactly a function of event separation, r_ij, then one could calculate the relative location of the group of events based only on their waveform similarity at a single station. However, only the shape and not the orientation or overall position of the cluster can be determined, since the data depend only on the inter-event distances. Furthermore, the shape is only determined up to a mirror-reflection (i.e. inversion). We note that the inversion process cannot simultaneously determine the scale factor, s. It must either be known a priori (e.g. through array measurements) or set to an arbitrary value (in which case the results contain only shape and not size information).

Inversion Algorithms and Tests

The algorithm for reconstructing the shape of the cluster of events from the correlation coefficients is very simple when the data are perfect: The inter-event distances are given by r_ij = -s ln(C_ij). One begins by forming a tetrahedon with the first four events, with edges of length r₁₂, r₁₃, r₂₃, r₁₄, r₁₂, and r₃₄. The choice of whether to put the fourth event above or below the plane of the first three selects between the two mirror-reflections. Subsequent events are added, one by one, by forming additional tetrahedra that share a face with the initial tetrahedron. For these subsequent tetrahedra, only one of the two possible positions (above or below the face) will satisfy all the r_ij.

In practice, noise usually precludes the use of this reconstruction method, since it introduces inconsistencies in the r_ij. The problem is overdetermined, in the sense that O(N²) observations are available to determine O(N) unknowns. An error-minimization technique is thus warranted. We seek to determine a set of earthquake locations, x⁽ⁱ⁾ such that the predicted correlation coefficients:

C_ij^pre = exp( -r_ij/s ) ; r_ij = |x⁽ⁱ⁾-x^(j)|

match the observed coefficients, C_ij^obs. An exact fit will not be possible in the presence of noise. We will seek instead to find the x⁽ⁱ⁾ that minimize the misfit:

E = |C_ij^obs-C_ij^pre|

Note that we use the L₁ (absolute value) norm, instead of the more typically used L₂ (least squares) norm, in order to supresses the influence of data outliers. We use a Monte-Carlo method to solve this inverse problem. The scale factor is arbitrarily taken to be unity, recognizing that the solution can be arbitrarily rescaled. The event locations, x⁽ⁱ⁾, are initially assigned random values within a source three-dimensional volume, V, which is chosen to be large enough so that it does not constrain the final event distribution (a cube with edges of N times the maximum r_ij would be sufficient). The locations are then randomly changed, with a new set of locations being accepted only if the misfit, E, decreases. We find that randomly alternating between the following strategies leads to rapid convergence of the solution (i.e. trapping by local minima is avoided): randomly assigning a single x⁽ⁱ⁾ to a new position in V; randomly moving a single x⁽ⁱ⁾ a small increment, dx^s; randomly moving a single x⁽ⁱ⁾ a large increment, dx^l; randomly moving a cluster of neighboring x⁽ⁱ⁾ a small increment, dx^s; randomly rotating a cluster of neighboring x⁽ⁱ⁾ about one of its members; randomly inverting a cluster of neighboring x⁽ⁱ⁾ through a randomly chosen axis. Our experience is that about 10⁵ iterations are necessary when N=O(100), which can be accomplished in a few minutes on a computer workstation. A C-language program that implements the inversion method is available at URL:

http://doherty.ldeo.columbia.edu/users/menke/eqloc/clocate.tar.Z

We have tested this method on a synthetic dataset of 64 events, arranged in a 8 by 8 grid with 1 m spacing on a planar fault (Figure 1A). The synthetic data (i.e. correlation coefficients, Figure 2) are computed from the earthquake location using the formula C_ij = exp( -r_ij/s ), where s is assumed to have the known value of unity. The initial event locations are randomly assigned within a 100x100x100 m³ cubic source volume. After 10⁵ iterations, the relative locations of the events are well recovered (Figure 1B), with a 99% improvement in misfit (with respect to the random locations). In particular, the fact that the events all lie on a 2D plane within the 3D volume is clearly detected.

We have also applied this method to some actual seismic data (Figure 3). In order to provide a means of verifying the solution, we locate the eleven stations of a linear array that has recorded a single regional earthquake. The principle of reciprocity indicates that the seismograms are the same as eleven events, with the same spacing as the array elements, recorded on a single station. We can thus compare the estimated array element locations with the known ones. The data (i.e. C^obs; Figure 4) shows that, as expected, waveform similarity declines with the distance between stations, although some statistical variability is evident. The starting model is taken as random locations in a 100x100x100 m³ cubic three-dimensional source volume, and the scale factor, s, is arbitrarily set to 1 m. The solution, which reduces the misfit by 95% with respect to the initial, random locations, correctly recovers the linearity of the event locations and their relative order (Figure 5).

Adaptation of Traveltime Inversion Algorithms and Conclusions

While the idea of single-station earthquake relocation method based on correlation coefficients alone is intriguing, a more accurate result would be acheived by combining the correlation data with traveltime data. Any traveltime-based relocation algorithm that is based on some form of linearized traveltime inversion (i.e. Geiger's method) can easily be adapted to include correlation coefficient data, since the Frechet derivatives that express their change with earthquake location and scale factor can be trivially computed:

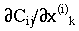= - (x⁽ⁱ⁾_k - x^(j)_k) exp(-r_ij/s)/(r_ijs)

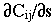= r_ij s^-2 exp(-r_ij/s)

Here we have assumed that the scale factor, s, is being determined as part of the inversion process (which is now possible since the traveltime data provide information on the overall length scale of the cluster of events). Regional variations of this scale factor, which is a measure of heterogeneity in the earth, may also be of interest.

Acknowldgements. This work arose out of a discussion on correlation matrices that I had with Marc Spiegelman, whom I thank. Lamont-Doherty Contribution Number 00000.

References

Got, J.-L., J. Frechet and F.W. Klein, Deep fault plane geometry inferred from multiple relative relocation beneath the south flank of Kilauea, J. Geophys. Res., 15,375-15,386, 1994.

Menke, W., A. Lerner-Lam, B. Dubendorff and J. Pacheco, Polarization and coherence of 5-30 Hz seismic wave fields at a hard rock site and their relevance to velocity heterogeneities on the crust, Bull. Seism. Soc. Am. 80, 430-449, 1990.

Menke, W., A. Lerner-Lam and R. Mithal, Spatial coherence of 5-25 Hz seismic wavefields at a hard rock site, Structural Safety 10, 163-179, 1991.

Nadeau, R.M., W. Foxall and T.V. McEvilly, Clustering and periodic recurrence of microearthquakes on the San Andreas fault at Parkfield, CA, Science 267, 503-506, 1995.

Phillips, W.S., L.S. House and M.C. Fehler, Detailed joint structure in a geothermal reservoir from studies of induced microearthquake clusters, J. Geophys. Res. 102, 11,745-11,763, 1997.

Shearer, P.M., Evidence from a cluster of small earthquakes for a fault at 18 km depthbeneath Oak Ridge, Southern California, Bull. Seism. Soc. Am. 88, 1327-1336, 1998.

Slunga, R., S. Rognvaldsson and R. Bodvarsson, Absolute and relative locations of similar events with application to microearthquakes in southern Iceland, Geophys. J. Int. 123, 409-419, 1995.

Figure Captions

Figure 1. A)Test pattern of 64 earthquake hypocenters, arranged in a 8 by 8 grid with 1 m spacing on a planar fault. B) Relative location of the hypocenters in A) based on correlation coefficient data. Note that the relative locations have been correctly recovered.

Figure 2. Correlation coefficient matrix, C_ij, for the data in Figure 1. Each element of the matrix is represented by a circle whose diameter scales with the value of the correlation.

Figure 3. P wave seismograms from a regional event observed on a linear array in Kazakstan. The station spacing is 2 km. (Data courtesy of W.Y. Kim)

Figure 4. Correlation coefficent matrix, C_ij for the seismograms shown in Figure 3. Each element of the matrix is represented by a circle whose diameter scales with the value of the correlation.

Figure 5. A) Actual locations, with symbol size indicating order. B) Locations determined by inverting correlation coefficient data in Figure 4. Note that the linear shape has been recovered.