Environmental Data Analysis BC
ENV 3017
Statistics 2a
Probability
- relative frequency = Number of times an event
occurs/number
of replications
- probability = relative frequency on an event after an
indefinitely
long number of trials
Probability distributions
- pattern of probabilities for a set of events is called a probability
distribution
- two important elements:
- the probability of each event or combination of events must
range from
0 to 1
- the sum of the probabilities of all possible events must be
equal to 1
- discrete probability distribution => probabilities
associated with
series of discrete outcomes
- e.g. for a six sided die: p(y)
= 1/6, y=1,2,3,4,5,6
- continuous probability distribution => probabilities
associated
with continuous values
- we cannot assign a positive probability to a specific value
- continuous probability distributions are calculated using a
probability
density function
- the probability associated with a range of values is equal to
the area
under the PDF (probability density function) curve
- Distributions tutorial, we'll focus
on the Normal distribution
Random Variables and random samples
- a random variable is a variable whose values occur at
random,
following
a probability distribution
- when a random variable attains a value that value is called an observation
- a collection of observations is called a random sample
- Random sample tutorial (Marksman/target)
- larger samples result in histograms
resembling the PDF more closely
The Normal Distribution
- the distribution used in the above example is the Normal
distribution:
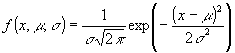
- µ
is the true mean, σ the true standard deviation, x the random
variable
- Probability tutorial => normal
distribution
- last pageof tutorial: find the
probability
between
±1σ and ±2σ.
(~0.68 and 0.95)
- the normal curve is
symmetric
about
the average, and the total area under it is 100% (fig).
- Standard units say
how
many sigma’s
a value is, above (+) or below (-) the average.
- How to normalize the
histogram: x (height in inches) becomes (x-µ)/σ, and
the y-axis changes from %/inch to %/standard unit (fig).
- many histograms have roughly
the
same
shape as the normal curve.
- the main reason why the normal distribution is a good
approximation to
many experiments in the sciences is the Central Limit
Theorem:
"As the sample size, n, increases, the sampling distribution of the
mean
approaches a normal distribution, no matter how the population being
sampled
is distributed".
- if a list of numbers follows
the
normal
curve, the percentage of entries falling in a given interval can be
estimated
by converting the interval to standard units and then finding the
corresponding
area under the normal curve. As already mentioned above, about 68% of
the observations in a large sample within one σ of the average, and
about
95% are within two σ's of
the average.
Parameters and estimators
- the normal distribution is described by two parameters, µ
and σ
- these parameters can be estimated by the mean
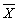 and standard deviation SD
and standard deviation SD
- how large must the sample be to properly estimate µ?
- example: 50 samples with 100
observations
each
sampled
from a normal distribution (µ = 0, σ = 1),
the mean of means close to 0, and the SD of the means is ~1/10 of the σ
of the original normal distribution
- (Population parameters tutorial)
- how to find out if data are normally distributed?
- use StatPlus to generate random normal data
- display data in two ways (using StatPlus)
- as histogram with normal distribution overlay
- as normal probability plot (normal score is the value
you would
expect if your sample came from a normal distribution, think of an
infinite
number of samples, each consisting of 100 observations, and average the
lowest number, the second lowest and so forth)
- the SD of
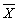 is also referred to as the Standard Error (SE) of
is also referred to as the Standard Error (SE) of 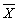
- by increasing the sample size, we can reduce SE
- Central limit theorem
- the central limit theorem describes the sampling distribution
of the
sample
average
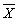 ,
taken from any distribution
,
taken from any distribution
- If each observation follows a distribution with a mean µ
and standard deviation, σ, the Central Limit theorem states that the
distribution of the sample averages approximately folows a Normal
distribution with a mean, µ, and standard deviation of σ/n1/2
(where n is teh smaple size). This theorem is true for any
distribution, as long as th mean and standard deviation of the
distribution exists and are finite.
- (Central limit theorem tutorial)
Standard Error
A repetition of an experiment will
result
in variable results. Imagine, for example, a multiple repetition of an
ozone concentration measurement. What is the error of your average
ozone
concentration? The more measurements you do (the larger n) the more precise
the
average should be.
The standard error of the average
(SE) is:
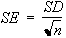
SE is therefore a measure of how precise the mean 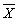 is
an estimator of the sample averageµ . Statistical theory tells is
(for large n) that a band around the sample mean of +/- 2 SE will
include the value of µ, 95% of the time. FOr example if the
sample average is 0 and the SE is 0., we can be 95% confident that teh
value of µ lies somewhere between -0.2 and 0.2. We don't know the
exact value of µ, but we have narrowed teh range of likely
values. By increasing teh sample size n, we can make the band as narrow
as we wish.
is
an estimator of the sample averageµ . Statistical theory tells is
(for large n) that a band around the sample mean of +/- 2 SE will
include the value of µ, 95% of the time. FOr example if the
sample average is 0 and the SE is 0., we can be 95% confident that teh
value of µ lies somewhere between -0.2 and 0.2. We don't know the
exact value of µ, but we have narrowed teh range of likely
values. By increasing teh sample size n, we can make the band as narrow
as we wish.
Resources:
- Freedman, D., Pisani, R.,
Purves, R.,
and Adhikari, A. (1991) Statistics. WW Norton & Company, New York,
2nd ed. 514pp.
- Fisher, F.E. (1973)
Fundamental
Statistics
Concepts. Canfield Press, San Francisco, 371 pp.
- Berenson, M.L., Levine,
D.M.,
and Rindskopf,
D. (1988) Applied statistics - A first course. Prentice Hall, Englewood
Cliffs, NJ, 557pp.
- Lyons, L. (1991) A practical guide to data analysis for physical
science
students. Cambridge University Press, Cambridge, UK, 95p. (Barnard QC
33.L9
1991 c.1)
- Hartwig, F., and Dearing B.E. (1979) Exploratory data anlaysis.
Sage
University
Paper series on Quantitative Applications in the Social Sciences, 16,
Sage
Publcations, Beverly Hills and London, 83p. (Barnard HA 29.H257 c.1)
- Jaffe, A.J., and Spirer, H.F. (1987) Misused statitistics.
Popular
statistics,
5. Marcel Dekker, Inc., New York, 236p. (Barnard HA 29.J29 1987)
- Knoke, D., and Bohrnstedt, G.W. (1991) Basic social statistics.
F.E.
Peacock
Publishers, Inc., Itasca, Illinois, 363p. (Barnard HA 29.K735 1991 c.2)
- Levin, J., and Fox, A.J. (1994) Elementary statistics in social
research.
Harper Collins College Publishers, New York, 508p. (Barnard HA 29.L388
1994 c.1)
- Welkowitz, J, Ewen, R.B., and Cohen, J. (1991) Introductory
statistics
in the behavioral sciences. Harcourt Brace & Company, Orlando,
Florida,
391p.
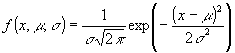
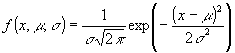
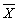 and standard deviation SD
and standard deviation SD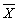 is also referred to as the Standard Error (SE) of
is also referred to as the Standard Error (SE) of 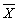
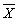 ,
taken from any distribution
,
taken from any distribution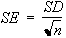
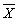 is
an estimator of the sample averageµ . Statistical theory tells is
(for large n) that a band around the sample mean of +/- 2 SE will
include the value of µ, 95% of the time. FOr example if the
sample average is 0 and the SE is 0., we can be 95% confident that teh
value of µ lies somewhere between -0.2 and 0.2. We don't know the
exact value of µ, but we have narrowed teh range of likely
values. By increasing teh sample size n, we can make the band as narrow
as we wish.
is
an estimator of the sample averageµ . Statistical theory tells is
(for large n) that a band around the sample mean of +/- 2 SE will
include the value of µ, 95% of the time. FOr example if the
sample average is 0 and the SE is 0., we can be 95% confident that teh
value of µ lies somewhere between -0.2 and 0.2. We don't know the
exact value of µ, but we have narrowed teh range of likely
values. By increasing teh sample size n, we can make the band as narrow
as we wish.