Environmental Data Analysis BC
ENV 3017
Statistics 2b
Confidence Intervals
- Review of the Central Limit
Theorem as discussed last time
- We learned above that a sample average will approximately follow
a normal distribution with mean µ and standard deviation σ/n1/2.
- We also know that in a normal distribution, about 95% of the time
values fall within about 2 standard deviations of the mean.
- That means that we can construct a confidence interval ranging from
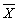 - 2*SE to
- 2*SE to 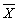 + 2*SE. The term 95% confident means that we are
confident that our procedure will 'capture' the value of µ 95% of
the times that it is used.
+ 2*SE. The term 95% confident means that we are
confident that our procedure will 'capture' the value of µ 95% of
the times that it is used.
- The factor of 2 is just approximate and only valid if our sample
size is large (n>25).
- For large samples, we can
calculate this factor (called the z-value) more precisely by
using the Excel NORMINV
function, it is 1.96. This factor will be
different when we look at small samples. Demonstrate of Excel
help feature with new functions.
- The z-value is the point on a Normal
curve such that the probability of a value being <z is equal to p.
- after defining alpha as
the
probability for being outside the interval we can define the exact
confidence interval as:

- Explore the confidence
interval tutorial
t-distribution and confidence intervals
So far we have assumed we know the standard deviation σ and that we are
dealing with large n (n>25). When
we
substitute σ by the
observed standard deviation SD then we cannot use
the normal distribution anymore, but need to use the Student t-distribution.
The t-distribution has one more parameter, the degrees of freedom
(sample size n -1).
- explore the t-distriution
in the distribution tutorial
The factor of '2' we have so far used has to be replaced by a 't-value'
derived from the t-distribution
we can then calculate the t confidence interval using the
t-distribution:
confidence interval: 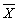 ± t-value * SE
± t-value * SE
The t-value can be calculated using the Excel function TINV (alpha,n-1).
For a 95% confidence interval and n=5 observations in a sample, for
example, it would be TINV(0.05,4) = 2.776. Again, we would then state
that with 95% confidence we think that our procedure captures the true
mean in the confidence interval.
Experimental errors
All experiments are characterized
by an experimental error.
There are two kinds of errors:
- random errors or statistical
errors
- replicate measurements yield
typically
slightly different results caused by variability within the natural
process
and the instrument
- results in a variation of the
measurements
around the ‘true’ (or ‘exact’) value
- precision of an
experiment refers
to this kind of error
- this is what we have been
talking about so far
- caused by not properly
calibrated instrument,
drifts etc.
- results in a systematic
difference between
measured and ‘true’ value
- accuracy of an
experiment refers
to this kind of error
In summary:
individual measurement = exact
value
+ bias + chance error
Each measurement result should be
given with its error. However, it is often very difficult to quantify
the
systematic error, and in most cases the given error is the statistical
error only. This error only states how precise an experiment
was
and not how accurate it was.
Error reporting
Errors are reported as absolute
or
relative
errors,
for example:
ozone concentration at West
Point,
8/3/1993, 14:00:
(125 ± 5) ppm or (125
±
4%) ppm
The error can be a standard deviation, a
SE (or 2*SE) or, e.g. a 95% confidence interval. You'll need to state
what your error bars reflect!
Error Propagation
In many cases you need to calculate
a value based on your measurement results using a formula. What is the
SE of the derived number? For formulas that only include only simple
mathematical
operations the propagation of errors is relatively simple. The
following
rule approximates the error of the derived number:
addition, subtractions =>
absolute error = Square root (sum of
(absolute
errors)2)
multiplication, division => relative error = Square root (sum
of
(relative
errors)2)
You can determine the error (D f)
of
a
more complex function f (x, y, z, ....) by using
the
partial derivatives of the function and the errors of the individual
variables
(D x, D y, D z,....):

Resources:
- Freedman, D., Pisani, R.,
Purves, R.,
and Adhikari, A. (1991) Statistics. WW Norton & Company, New York,
2nd ed. 514pp.
- Fisher, F.E. (1973)
Fundamental
Statistics
Concepts. Canfield Press, San Francisco, 371 pp.
- Berenson, M.L., Levine,
D.M.,
and Rindskopf,
D. (1988) Applied statistics - A first course. Prentice Hall, Englewood
Cliffs, NJ, 557pp.
- Lyons, L. (1991) A practical guide to data analysis for physical
science
students. Cambridge University Press, Cambridge, UK, 95p. (Barnard QC
33.L9
1991 c.1)
- Hartwig, F., and Dearing B.E. (1979) Exploratory data anlaysis.
Sage
University
Paper series on Quantitative Applications in the Social Sciences, 16,
Sage
Publcations, Beverly Hills and London, 83p. (Barnard HA 29.H257 c.1)
- Jaffe, A.J., and Spirer, H.F. (1987) Misused statitistics.
Popular
statistics,
5. Marcel Dekker, Inc., New York, 236p. (Barnard HA 29.J29 1987)
- Knoke, D., and Bohrnstedt, G.W. (1991) Basic social statistics.
F.E.
Peacock
Publishers, Inc., Itasca, Illinois, 363p. (Barnard HA 29.K735 1991 c.2)
- Levin, J., and Fox, A.J. (1994) Elementary statistics in social
research.
Harper Collins College Publishers, New York, 508p. (Barnard HA 29.L388
1994 c.1)
- Welkowitz, J, Ewen, R.B., and Cohen, J. (1991) Introductory
statistics
in the behavioral sciences. Harcourt Brace & Company, Orlando,
Florida,
391p.
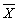 - 2*SE to
- 2*SE to 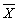 + 2*SE. The term 95% confident means that we are
confident that our procedure will 'capture' the value of µ 95% of
the times that it is used.
+ 2*SE. The term 95% confident means that we are
confident that our procedure will 'capture' the value of µ 95% of
the times that it is used. 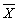 - 2*SE to
- 2*SE to 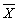 + 2*SE. The term 95% confident means that we are
confident that our procedure will 'capture' the value of µ 95% of
the times that it is used.
+ 2*SE. The term 95% confident means that we are
confident that our procedure will 'capture' the value of µ 95% of
the times that it is used. 
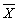 ± t-value * SE
± t-value * SE 