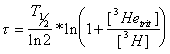Tritium/³He dating

1. General background

Tritium (³H or T) is the radioactive isotope of hydrogen that decays with a half life of 12.43 years to its stable daughter ³He. Tritium is produced naturally in the upper atmosphere by interaction of nitrogen, and, to a lesser extent, oxygen with cosmic rays. After oxidation to HTO, it takes part in the natural water cycle. Before the full potential of natural tritium as a tracer for water movement in natural systems could be explored its distribution was masked by addition of large amounts of so-called ‘bomb tritium’ produced during the surface tests of nuclear weapons. These tests which were mainly performed in the early 1960s, led to an increase of tritium in precipitation over the continents of the northern hemisphere from roughly 5 TU to levels of the order of 1000 TU. One TU (Tritium Unit) means a tritium to hydrogen ratio of 10^-18.

Whereas the addition of bomb tritium to the environment practically eliminated the use of natural tritium as a tracer, it offered a new tool, i.e., the use of the bomb tritium peak (Fig. 1) as a ‘dye’ that is delivered to natural water systems from the atmosphere on local to global scales. If the tritium delivery as a function of time can be reconstructed, this penetration process can be used for quantitative studies of water movement through identification of the bomb peak in certain ground water bodies. However, there are natural limits to this method because tritium decay and dispersion make it increasingly difficult to identify the bomb peak in groundwater.

These problems can be overcome by using tritium in combination with its decay product ³He (³He_trit) as first suggested by Tolstykhin and Kamensky and experimentally confirmed by Torgersen et al. Simultaneous measurement of tritium and tritiogenic ³He allow us (1) to identify the tritium peak as the sum of tritium and (³He_trit), [³H + ³He_trit], even if most of the tritium has decayed, and (2) to directly calculate an age from the radioactive mother/daughter ratio (tritium/³He age). Extensive studies of the methodology and applicability of tritium/³He dating were started in the mid/late 1980s and early 1990s.

2. Determination of the tritium/³He age

In principal, the determination of the tritium/³He age of groundwater is simple. If both the tritium and ³He_trit concentrations are measured in TU, it can be calculated as

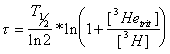(1)

The most difficult step in the determination of the tritium/³He age is the separation of ³He_trit from the total ³He (³He_tot) dissolved in a groundwater sample. The total ³He concentration has a variety of sources (equation (2)):

(2)

where ³He_eq = ³He in solubility equilibrium with the atmosphere, ³He_exc = ³He due to excess air [29] and ³He_terr = terrigenic ³He (nucleogenic ³He plus mantle ³He). In this equation, only ³He_tot and ³He_eq are determined through measurements. ³He_exc and ³He_terr (if present in the sample) have to be determined by using measurements of ⁴He and Ne (³He_terr). The total ⁴He concentration measured in a groundwater sample can be written as:
 

(3)

where ⁴He_tot = total measured ⁴He concentration in the groundwater sample, ⁴He_eq = ⁴He concentration in solubility equilibrium with the atmosphere, ⁴He_exc = ⁴He concentration caused by excess air, and ⁴He_terr = terrigenic ⁴He concentration (radiogenic ⁴He plus mantle ⁴He). If no terrigenic helium is contained in the groundwater sample, ³He_trit can be calculated by using equation 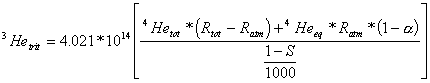(4):

(4)

where R_tot = measured ³He/⁴He ratio of the sample, R_atm = ³He/⁴He ratio of air (1.384*10^-6), a = solubility isotope effect (ca. 0.983)), and S = salinity in ‰. The conversion factor for ³He from cm³STPg^-1 to TU is 4.021*10¹⁴/[(1-S)/1000)] TU/cm³STPg^-1.

For separation of terrigenic helium, we have to use neon measurements. Assuming that neon has no sources other than the atmosphere, and that (Ne/⁴He)_exc = (Ne/⁴He)_air, we can calculate the terrigenic ⁴He component to be:

(5)

where Ne_tot = measured neon concentration in the sample, ⁴He_atm/Ne_atm = atmospheric He/Ne ratio (0.288), and (Ne_tot - Ne_eq) = Ne_exc = neon concentration originating from excess air.

³He_terr is calculated by multiplying ⁴He_terr calculated from equation (5) by the ³He/⁴He ratio of the terrigenic helium component. This component can be radiogenic helium, mantle helium, or a mixture of these two components. The most practical approach to determining R_terr is to measure it in groundwater samples from the same aquifer that are free of tritium. If there is no tritium-free groundwater in the studied aquifer, an estimate of R_terr can be obtained in most cases by plotting ³He versus ⁴He. Such a plot typically provides fairly good clues with respect to the origin of the terrigenic helium.

The atmospheric ³He component (³He_atm) can be written as:

(6)

Finally, ³He_trit is obtained from equation (7) [e.g., 2]:

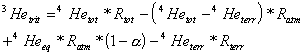(7)

3. Non-linearity of the tritium/³He age

The tritium/³He age formally calculated from equation (1) is an apparent age. It is independent of the initial tritium concentration of the water sample which is one of the advantages of the method because it eliminates the necessity to establish the exact time- dependent tritium delivery to the aquifer. A potential problem for the quantitative interpretation of the tritium/³He age is the fact that it is affected by mixing and dispersion. Due to this effect, the tritium/³He age is typically biased toward the age of the water component with the higher tritium concentration. Therefore, for quantitative studies, mixing has either to be ruled out as a major factor influencing the flow regime or it has to be accounted for in the data evaluation.

Significant differences between the apparent tritium/³He ages and the true water ages typically occur near the location of the bomb peak. The reason for this observation is due to the high tritium and ³He concentration gradients near the bomb peak and the related increased transport of both tracers by dispersive processes. This effect also determines the useful time period over which tritium/³He dating is typically applicable. In many aquifers, the tritium/³He balance below the bomb tritium peak is dominated by downward dispersion of bomb tritium and ³He_trit resulting from its radioactive decay. Therefore, in such cases, the tritium/³He age distribution is constant over a depth range of a few to several ten meters below the location of the bomb peak. However, in aquifers with very low dispersion rates, meaningful tritium/³He ages can be obtained for periods preceding the bomb peak.

4. Confinement of tritiogenic ³He

Because ³He is a gas, the application of the tritium/³He method to dating of groundwater depends strongly on the degree of confinement of ³He_trit in the groundwater. The confinement of ³He_trit is mainly determined by the ratio of advection to dispersion in water parcels moving away from the water table. It has been shown that for aquifers with reasonably high recharge rates (and related vertical flow velocities near the water table), loss of ³He_trit is smaller than about 10 to 20%.