Surface water and groundwater flow

Global water budget

• Earth's water inventory (Fig)
• groundwater in the hydrologic cycle (Fig)
• hydrological cyclereservoirs and fluxes (Fig)
• there is significant uncertainty in some of these numbers (Fig)
• residence times
  
• atmosphere: 2 weeks
• surface waters: 4 years
• groundwater: 20,000 years

Surface water flow

Forces on fluids

• the basic forces that make fluids move are gravity, pressure differences, and surface stresses
• pressure is a normal stress

Bernoulli equation

• let us look at the movement of a fluid in a pipe (Fig3.5)
• the statement of the conservation of energy for a frictionless fluid along a flowline is the following:
• p*V + m*g*z + 1/2*mu² = constant, means:
• work due to pressure + potential energy + kinetic energy
• by dividing this equation by m = v*r*g we get the Bernoulli equation:
• u²/(2*g) + z +p/(r*g) = constant, means:
• velocity head + elevation head + pressure head = total head
• this head can be measured by looking at the level to which the water rises in a vertical tube stuck into the pipe
• assumptions we are making:
• no friction (viscosity = 0)
• incompressible fluid
• homogeneous fluid
• flow steady with time
• example: expansion joint in a hose  (Fig3.7)
• apply continuity equation Q = u*A = const, then Bernoulli equation
• decrease of mean velocity results in increase of pressure
• experiment: blow on sheet of paper

Friction

• in reality, if we do an experiment, we do see a loss in head along a pipe due to friction (Fig3.8)
• instead of having a uniform value in the pipe, there is a velocity profile (Fig3.9)
• u²/(2*g) + z +p/(r*g) = constant needs to be modified to: u²/(2*g) + z +p/(r*g)  +h_L= constant
• the head loss can be described as: h_L = f*L*u²/(D*2*g), f being the friction factor
• the friction factor has been measured under a range of circumstances (Fig3.10 for smooth pipes)
• The key parameter to describe a flow situation is the Reynolds number: R = r*U*D/m
• at R>2000 something happens, the flow becomes turbulent
• Reynolds experiment, laminar ("layered")  flow, turbulent ("restless") flow (Fig3.11)
• is flow in a straw laminar or turbulent?
• let us calculate R for an example:
• U=2 m/s
• D = 0.03 m
• r = 10³ kg/m³
• m  = 1.139 10^-3 Pa s
• how can we make the flow laminar?
1. reducing the velocity;
2. reducing the diameter;
3. reducing the density of the fluid; or
4. increasing the viscosity. reduce

Flow in channels

• in most cases, friction does play a big role in stream flow, so we are actually loosing head in the flow (Roughness of a stream)
• flow in a channel is described by Manning's equation (Fig4.8):

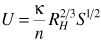
R_H=wh/(2h+w): Hydraulic radius
k=1 m^1/3s^-1
S: slope
n: roughness coefficient

Measuring flow in natural channels

• weirs can be used to measure discharge rates
  

• 

• we can look impirically at the discharrge rate vs. height relationship for a stream without a well-defined weir and can can use this to estimate the discharge rate (Fig4.13, for this particular creek the exponent in the empirical relationship between Q and h is 2.85).
• schematic diagram of a stream gaging station (Fig5.2)
• velocity distribution as a function of depth  (Fig4.10), most flow is turbulent, average flow velocity is at a depth of 0.6*total depth
• we can measure the discharge rate by taking measurements at 0.6* depth (from surface) wading through the river (Fig4.11)
• Q = U*A = S w_i*h_i*U_i
• Small stream gaging
• Gaging larger streams and rivers
• stream gaging on the Colorado River at Lee's Ferry
• Lee's ferry, just below Hoover Dam, boats ready for trip down the Grand Canyon
• gondula used for gaging the Colorado
• steel wire crossing the Colorado at Lee's Feey and monitoring station on the other side of the river

Groundwater

• groundwater is the water in the saturated zone (Fig) (Fig)
  
• recharge is the water entering the saturated zone
• in many parts of the world, groundwater is the only source of fresh water
• in the US about 10% of the rainfall becomes groundwater eventually. This amount equals the annual use of water in the US, about 3 inch per year
• Water use in the US (Fig)
• water may stay in the groundwater reservoir between several days and thousands of years. We will discuss tracer techniques that may be used to derive residence times later in the class
• management of catchment areas  requires understanding of groundwater flow
• many environmental issues involve groundwater

Conceptual model of groundwater flow

the flow of water through a porous medium (Fig 6.1)

water flows tortuous paths

geometry of channels is very complex

frictionles flow is totally meaningless!

conceptual model of flow through a porous medium is flow through a bundle of very small (capillary) tubes of different diameters (Fig 6.2)

the flow (Q) through a horizontal tube can be described as: Q = -p*D⁴/(128*m)*dp/dx (Poiseuille's law)

=> size of the capillary tubes is important!

Darcy's law

• what drives groundwater flow?
• water flows from high elevation to low elevation and from high pressure to low pressure, gradients in potential energy drive groundwater flow
• two ways how to derive the potential energy:
• 1: Bernoulli
• Bernoulli equation said: u²/(2*g) + z +p/(r*g) = constant, means: velocity head + elevation head + pressure head = total head
• in groundwater flow, we cannot make the assumption that there is no friction, therefore the  head is not constant
• also u is so small that that term can be typically neglected
• 2: direct determination of potential energy
• lifting up a parcel of water: W₁=m*g*z
• creating space for it in the groundwater system: W₂=p*V
• total work/m = g*z + p/r or h =  z + p/rg
• groundwater flows from high to low  head
• how do you measure the head or potential? => drill an observation well, the elevation of the water level in the well is a measure of the potential energy at the opening of the well: h=z + p/rg = z + F/(Arg) ......
• in 1856, a French hydraulic engineer named Henry Darcy published an equation for flow through a porous medium that today bears his name (Fig. 6.3)
• Q = KA (h₁-h₂)/L or q = Q/A = -K dh/dl, h: hydraulic head, h = p/rg + z
• q = Q/A is the specific discharge [L/T], dh/dl is the hydraulic gradient
• K is the hydraulic conductivity [L/T]
• the law is very similar to Ohm's law for electrical curcuits I = 1/R * U (current = voltage divided by resistance)
• the orginal Darcy experiment yielded these data (Fig 6.4)
• the analogy between Darcy's law and Poiseulle's law suggests that K = (const*d²)*rg/m
• the first term (const*d²) is k, the intrinsic permeability [L²], summarized the properties of the porous medium, while rg/m describe the fluid
• hydraulic conductivities and permeabilities vary over many orders of magnitude (Fig 6.5)

Example: calculation of a typical hydraulic gradient of 1/100 in a salt formation with a hydraulic conductivity of 10^-10 m s^-1 will produce a specific discharge of 10^-12 m s-1, or less than 1 mm per 30 years!
• specific discharge has the dimension of a velocity, but it is not the velocity at which the water flows in the porous medium, the water has to squeeze through the pores
•  tagged parcels that are averaged together, will appear to move through a porous medium at a rate that is faster than the specific discharge
• porosity is the fraction of a porous material which is void space f = V_void/V_total
• the mean pore water velocity is then: v = q/f (Fig)
• Darcy's law has been found to be invalid for high values of Reynolds number and at very low values of hydraulic gradient in some very low-permeability materials, such as clays.
• example :
• K= 10^-5 m/s, h₂-h₁ = 100m, L = 10km, A = 1m² > Q = 3.15 m³/y; the K value above is typical for a sandstone aquifer
• the actual flow velocity v may be calculated with the following formula: v=Q/(A*f)=q/f, f is the porosity, and q the specific discharge
• if the porosity n is 30%, the flow velocity in the example above is 10.5 m/y

Resources

Freeze, R.A. and Cherry, J.A. (1979) Groundwater. Prentice Hall, 604p.

Hornberger, G.M., Raffensberger, J.P., Wiberg, P.L., and Eshleman, K.N. (1998) Elements of physical hydrology. Johns Hopkins University Press,  Baltimore, 302p.

see also BC 3025 Hydrology class