Single seismogram estimates are needed to investigate the variation of splitting parameters with S-wave propagation direction. We use the cross-correlation method to find the parameters that best fit the model that the S-wave is composed of two pulses of identical shape but orthogonal polarization, one delayed with respect to the other.
Let us suppose that the S-wave polarization lies with the UV plane of
a cartesian UVW coordinate system. For weakly anisotropic material,
such as the Earth's mantle, the propagation direction will then be
nearly parallel to W. In general, one might need to establish the
relationship between this coordinate system and the usual
north-east-vertical coordinate system used to collect seismic data.
However, the SKS and SKKS core phases typically used in studies of
upper-mantle anisotropy have steep incidence angles, so that the
UV plane is nearly horizontal (typically within 
at the surface).
The vertical component of the seismogram is often
contaminated with compressional wave reverberations, so we believe it is
best to use only the horizontal component data. The resulting
measurement of splitting direction will be slightly biased by this
approach. However the effect of this bias on earth models can be
avoided simply by comparing these data to synthetic data oriented in the
same fashion.
We seek to find a rotation 
in the UV plane, and a delay 
that
maximizes the cross-correlation:
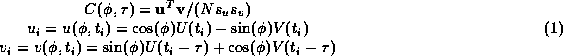
where 
and 
are the root mean squared amplitudes of horizontal component seismograms
u and v,
respectively, and 
, where 
is the sampling interval of
the seismogram.
After grouping the splitting parameters into a vector 
, we denote the cross-correlation as 
.
We estimate the best-fitting vector 
using a coarse grid
search followed by refinement with an interpolation algorithm.
We use a grid spacing of in and in .
We fit (using least-squares) the cross-correlation at the maximal node
and its nearest neighbors with a bi-quadratic function:
where A, B, C, ... F are constants.
The maximum of 
occurs at
, or:
Numerical tests (not shown) indicate that this technique locates the
maximum cross-correlation within 
% of the grid spacing, at
least for seismograms with the spectral characteristics of typical
SKS phases.
The uncertainty of the splitting parameters can be
calculated by comparing this problem to the linearized inverse problem
. Here the goal is to estimate model parameters m
and their covariance 
from a data vector d.
A simple least-squares estimate of the model parameters, ,
minimizes the misfit function
Here 
is the mean-squared amplitude of the data.
If the data have uncorrelated error with variance 
, the
variance of the estimated model parameters is related to the curvature of the
misfit function:
(see Menke [1989], eqn 3.52).
This equation quantifies the notion that narrow minima are associated
with precise estimates.
The ratio 
can be interpreted as the signal-to-noise
ratio 
.
We apply this formula to maximize the coherence between two seismograms u and v, each of length N. The misfit function is
where and are the root mean squared amplitudes of u and v, respectively.
This definition of misfit is algebraically equivalent to E=1-C, where
is the cross-correlation between the
two data series.
The variance of m is given by:
where r is the signal-to-noise ratio (assumed the same on the two seismograms).
We estimate the second derivative matrix by differentiating the
quadratic interpolant (2) of the cross-correlation .
The signal-to-noise ratio can be estimated from the value of C
itself, by assuming that deviations from perfect correlation are caused
entirely by stochastic noise in the seismograms.
Denoting this noise as 
and 
, and 
and 
as noise-free seismic signals, we have:
We assume that the noise-free and are scaled
versions of each other.
The expected value of the cross-correlation is
The estimated signal-to-noise ratio is thus 
.
Most time series are oversampled, and thus have correlated noise.
For this case N in (3) must be replaced with the degrees of freedom
:
The degrees of freedom can be estimated by computing the autocorrelation of the normalized misfit
The ratio 
is approximately the width of the main peak in the autocorrelation of 
.
We have tested this method of computing covariance against Monte Carlo
simulations using synthetic SKS phases that have prescribed
signal-to-noise ratios in the 1:1 to 100:1 range. The results (not
shown) indicate that the above methodology yields accurate
estimates of variance. Standard deviations generally agree with
Monte Carlo results to within 20-30%.
Standard deviations are typically 
for the fast axis azimuth,
and 
s for data used in this study (Figure 6).