Experiments with full datasets
Experiments with sparse datasets
References
Global three-dimensional (3D) velocity models of the Earth's mantle continue to evolve and become parameterized
on an ever finer scale. Models of both compressional and shear wave velocity are now commonly parameterized in terms
of constant velocity blocks [e.g., Vasco and Johnson, 1998; Grand et al., 1997; van der Hilst et al., 1997; Boschi
and Dziewonski, 1999] rather than spherical harmonic functions. Such ``high-resolution'' models, using blocks with sizes
on the order of a few hundred kilometers, have provided sharper images of coherent smaller scale heterogeneities,
in particular fast, sheet-like anomalies presumed to correspond to slabs penetrating into the lower mantle. These models
should lead to better characterization of P wave residuals for paths through subduction zones or other areas where small-scale lateral
heterogeneities are present.
However, a number
of factors may lead to lower resolution of large-scale, smaller amplitude anomalies in block models. Because
of the higher number of unknown parameters, it is still impractical to invert combinations of very large
data sets (waveforms and travel times), as is frequently done with spherical harmonic models [Su and Dziewonski, 1997; Li and
Romanowicz, 1996]. This may result in lower resolution in certain areas (particularly the shallow mantle) to which
particular data sets are sensitive.
In addition, the division into arbitrary, constant velocity blocks may induce an unrealistic
shape in long-wavelength anomalies. A lack of correlation between new, high-resolution Earth models and earlier
longer wavelength models has previously been noted [ Grand et al., 1997]. Another possible factor in this discrepancy
may be the use of regularization or damping in the solution of the inverse problem [Boschi and Dziewonski, 1999].
In this paper we use essentially the same set of test events as that used by Smith and Ekström [1996],
with additional explosions from the Chinese Lop Nor test site. The list of events includes 30 explosions in addition to 82 well-located earthquakes.
Only teleseismic P-wave arrivals in the distance range 25-96o. In addition to a correction for the mantle model, we apply a
crustal correction calculated for the model CRUST5.1 of Mooney et al. [1998].
We test the improvement which can be obtained
in teleseismic event location using the newer block models of mantle $P$ wave velocity compared to spherical harmonic models and to PREM.
The models are:
Introduction
Mislocation vectors for the test events in models SP12 and and BDP98 are compared in Figure 1. The much smaller location errors for explosion events, even compared with earthquakes located nearby, is obvious. The general trend for location errors using BDP98 to be larger than those using SP12 exists for all regions. Locations derived from BDP98 are generally displaced from the true location in the same direction as those derived from SP12, although by larger distances. This suggests that the amplitudes of large velocity anomalies are not as well recovered in BDP98, although the lateral positions of the anomalies are similar to SP12.
Figure 1. Mislocation vectors for the test events using the complete ISC P wave travel time set, for models SP12 (top) and BDP98 (bottom) without station corrections. Length of the vectors is proportional to the magnitude of the mislocation. The base of each arrow is plotted at the ground truth location and each vector points in the directon of the model-derived location. Explosion events are plotted as the solid vectors and earthquakes as the open vectors. Events located with BDP98 are generally mislocated in the same direction as with SP12, but with a larger error.
One area in which the location difference between BDP98 and SP12 is especially large is in the western United States. It is interesting to compare residuals predicted for these two models for events in this region. Although the areas for which the two models predict particularly large residuals are similar (Figure 2), in general the amplitudes of the residuals predicted by SP12 are larger. In contrast, the residuals predicted by both models for events at the Semipalatinsk nuclear test site are much more similar, although some differences (notably in north Africa and Australia) do exist. As a result the locations derived from both models for events in central Asia are quite similar.
Figure 2
It is important to examine the performance of 3D models when locating events teleseismically with a limited number of phases. The primary seismic network of the International Monitoring System, for example, is to consist of only 50 3-component stations and arrays worldwide. Station coverage in many areas is therefore sparse. In this section we discuss location experiments using only subsets of the available P wave data set.
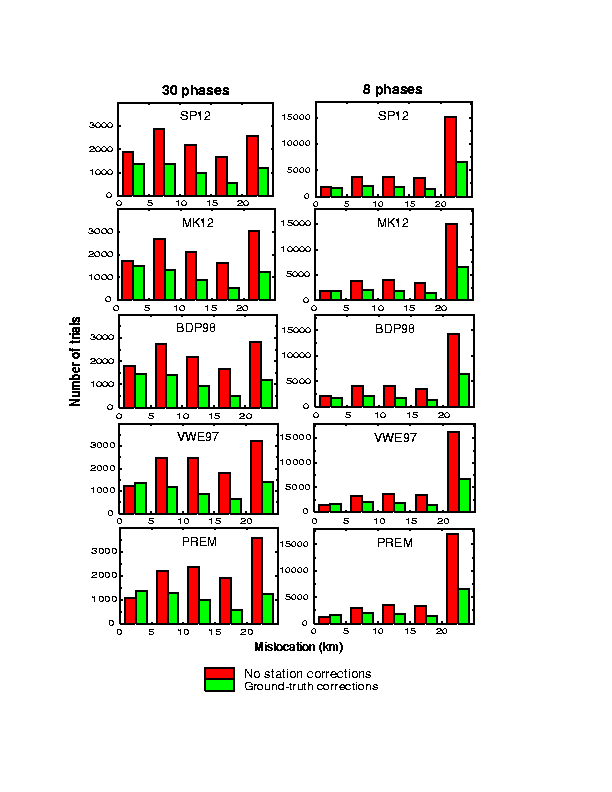
For each of the test events we randomly selected 30 of the available phases and relocated the event according to the procedure described above. We repeated this procedure 100 times for each event. No consideration with regard to the aziumth or epicentral distance of the reporting station was made when selecting the phases, except that the distance was restricted to between 25o and 96o. A location trial is deemed to be ``successful'' if it results in a location within the 1000 km2 circular area surrounding the actual location specified by the CTBT. Formal calculation of error ellipses often results in areas of less than 1000 km2 uncertainty which may not include the ground-truth epicenter. However, for the purposes of the CTBT, the area set aside for on-site inspection would include the true epicenter in these cases.The breakdown of the location trials is summarized in the following figure and tables. When using no station corrections and 30 total phases, the percentage of successful trials is 65-70%, and the average mislocation is only slightly greater than that obtained using all of the phases (Table 1). If ground-truth (empirical) calibration information is available, then an event can be located at a confidence level of 75-80% within the goal of the CTBT. This is even true when using PREM as the location model. If only 8 phases are used in the inversion, fewer than half of the trials are successful and the average mislocation increases to over 30 km for all of the 3D models.
Table 1. Average mislocation in km for location trials using a random selection of 30 phases. Results in column 2 were obtained using the 3-D mantle model only, for columns 3 and 4 station corrections based either on the model-derived location for the event or on the ground-truth location of a nearby event were applied to each phase used, respectively. 100 location trials were performed for each of the test events. Numbers in parentheses are the percentage of "successful" location trials for each case.
Table 2. Similar to Table 1 but for trials using only 8 phases. 250 trials were performed for each test event.

The figure displays the number of trials with location errors in 5 km bins as well as greater than 20 km. Again, the distribution of the location trials is similar for three of the 3D models with VWE97 giving slightly larger errors. Use of ground-truth information results in ~50% of the trials having a location error of less than 10 km (with 30 phases). In this case, the distribution of the location errors using PREM is almost exactly the same as using one of the 3D models. In the absence of calibration information, however, the quality of the locations derived from the 3D models is clearly superior. Without station corrections, the median mislocation is roughly 12 km using 30 phases and 20 km using 8 phases.
To some extent, the results from the location trials with sparse data sets are encouraging in that small to moderate teleseismic events may be located to within the specified 1000 km2 area for the CTBT about two-thirds of the time. The median mislocation in such circumstances is around 12 km. This is true even if calibration information is not available for any of the stations. Further improvement may be possible if care is taken to ensure that sufficient observations are used from all azimuthal quadrants, which we have not done in this study. The probability of achieving this accuracy is increased to over 75% if calibration information is available.
Enough data seems to be currently available to conclude that, while all 3D models of mantle velocity seem to provide substantial improvement over 1-D models in the ability to locate teleseismic events, the degree of improvement does not necessarily increase with the complexity of the model. Since it appears that neither the parameterization chosen for the tomographic inverse problem, nor the particular inversion technique used affect in large degree the solution obtained [Boschi and Dziewonski, 1999], some other explanation for this result should be invoked. For example, the type of regularization and damping employed in the inversion for block models with non-uniform data coverage might result in much lower amplitude anomalies in regions where the coverage is relatively low. This might lead to a tendency for block models to underpredict the range of observed residuals for events in some regions, such as we observe in Figure 2.Boschi, L. and A. M. Dziewonski, High and low-resolution images of the Earth's mantle: Implications of different approaches to tomographic modeling, J. Geophys. Res., 104, 25,567-25,594, 1999.
Engdahl, E. R., R. D. van der Hilst, and R. P. Buland, Global teleseismic earthquake relocation with improved travel times and procedures for depth determination, Bull. Seism. Soc. Am., 88, 722-743, 1998.
Grand, S. P., R. D. van der Hilst, and S. Widiyantoro, Global seismic tomography: A snapshot of convection in the Earth, GSA Today, 7(4), 1-7, 1997.
Li, X. and B. Romanowicz, Global mantle shear velocity model developed using nonlinear asymptotic coupling theory, J. Geophys. Res., 101, 22,245-22,272, 1996.
Mooney, W. D., G. Laske, and T. G. Masters, CRUST 5.1: A global crustal model at 5o x 5o, J. Geophys. Res., 103, 727-747, 1998.
Smith, G. P., and G. Ekström, Improving teleseismic event locations using a three-dimensional earth model, Bull. Seism. Soc. Am., 86, 788-796, 1996.
Su, W. and A. M. Dziewonski, Joint 3D inversion for P- and S-velocity in the mantle, EOS, 74, 557, 1993.
Su, W. and A. M. Dziewonski, Simultaneous inversion for 3D variations in shear and bulk sound velocity in the mantle, Phys. Earth Plan. Int., 100, 135-156, 1997.
van der Hilst, R. D., S. Widiyantoro, and E. R. Engdahl, Evidence for deep mantle circulation from global tomography, Nature, 386, 578-584, 1997.
Vasco, D. W. and L. R. Johnson, Whole Earth structure estimated from seismic arrival times, J. Geophys. Res., 103, 2633-2671, 1998.