Introduction
The global atmospheric
concentration of CO2
has increased
dramatically as a result of human activities since 1750 and now far
exceeds pre-industrial values. Indeed, present-day CO2
levels are
higher now than at any time in the past 650,000 years. The reason we
care about
this increase of course is
because of
concerns over climate change. CO2 is a greenhouse gas (GHG).
That is, it absorbs outgoing longwave radiation and thus warms the
atmosphere. CO2 is not the only GHG that is increasing due
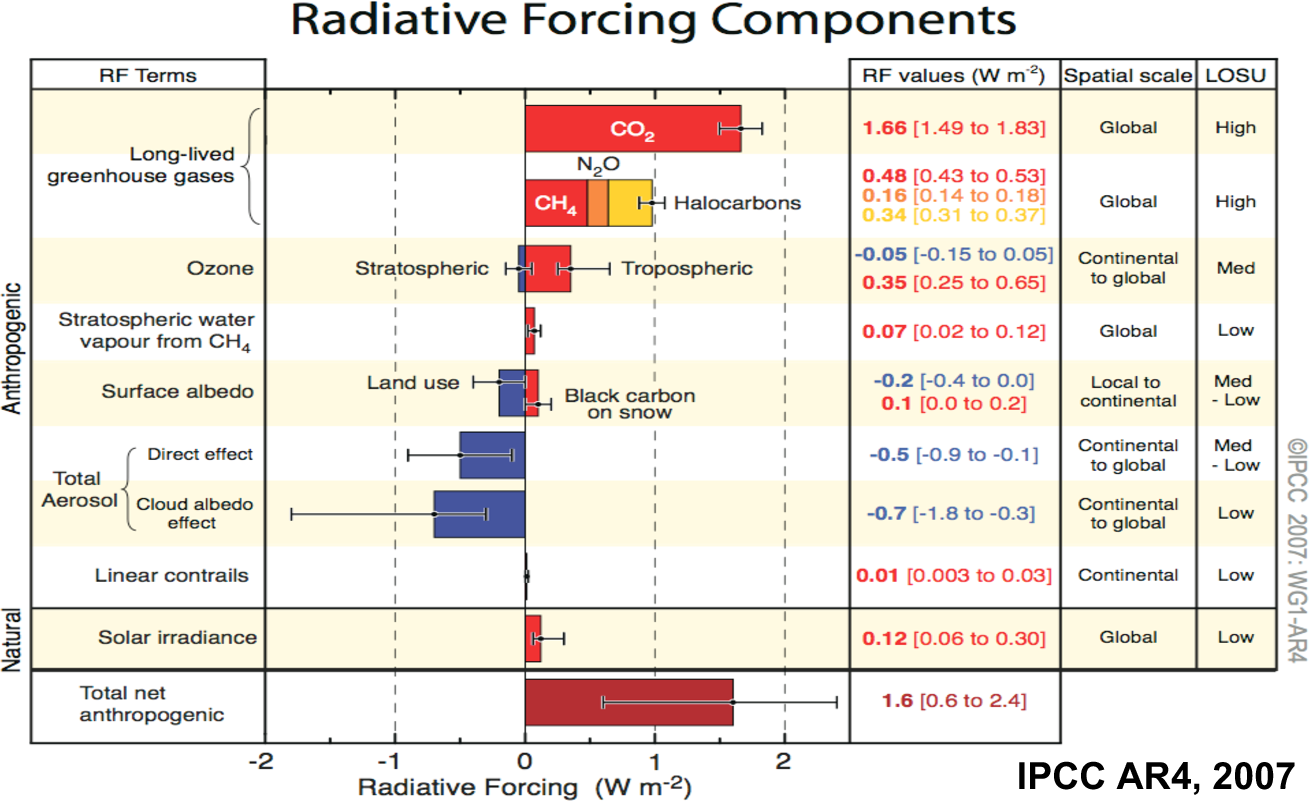
to human activity, but as the table from the IPCC report shows, its
radiative effect is greater than that of all other anthropogenic
GHG gases. Given the importance of CO2
for climate, a
key question
is where does this CO2 come from, and where does it go.
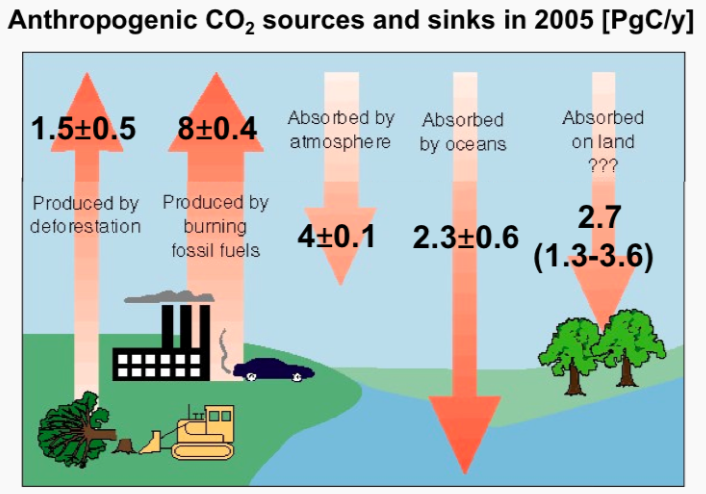
The
cartoon below attempts to summarize our current knowledge of the
sources and sinks of anthropogenic CO2. There are two
principal
sources. The largest is the burning of fossil fuels which emits on the
order of 8 PgC/y. (A petagram (Pg) is 1 billion metric tons.) The
second largest, at around 1.5 PgC/y, is changes
in land use,
primarily deforestation in the tropics to make way for agriculture.
Estimates for this source are relatively very uncertain however.
Together, these two sources contributed somewhere
between 370 to 610 PgC between the start of the industrial period
(nominally taken as 1765) and 2005. So what happened to this
CO2? Less than 50% of it, or 215 PgC, currently resides
in the atmosphere so the balance must have been taken up by the ocean
or the terrestrial biosphere. It is believed that the ocean sequesters
20 to 35% of manmade CO2 emissions and thus plays a
critical role in mitigating the effects of this perturbation to the
climate system. However, considerable uncertainties remain as to the
distribution of anthropogenic CO2 in the ocean, its rate of
uptake over the industrial era, and the relative roles of the ocean and
terrestrial biosphere in taking up manmade CO2.
To address these
questions, I and my colleagues, Francois Primeau at UC Irvine and Tim
Hall at NASA GISS, have reconstructed the first
spatially-resolved, time-dependent history of anthropogenic
carbon in the ocean over the industrial era. Our work is unique in many
ways. First, it is based solely on observations, and not on numerical
ocean models. Second, it provides the full 3-dimensional distribution
of anthropogenic CO2 in the ocean at any instant in time
between 1765 and the present. Third, our reconstruction resolves the
spatial distribution of the uptake of CO2 at the surface of
the ocean, thus identifying the most intense sinks of anthropogenic CO2
and their evolution over time. And last, the inverse method we have
developed to perform this reconstruction overcomes many of the
fundamental problems
and limitations that have plagued previous attempts at solving this
problem. Our reconstruction thus provides the first and most
comprehensive view of the ocean sink of manmade carbon and, by
combining with the known CO2 emission history, the
terrestrial biosphere sink. Thus, whereas before we had a single fuzzy
snapshot of manmade CO2 in the ocean, we now have a
relatively sharp movie that runs from the start of industrialization to
the present.
Estimating Anthropogenic CO2 in
the Ocean
The problem of estimating
anthropogenic
carbon (Cant) in the ocean has challenged scientists for
several decades. To understand why it is so difficult, it is useful to
review some basic aspects of the
problem. There are four key points to keep in mind:
- Anthropogenic carbon is not a directly measurable
quantity. It
has to be estimated using indirect means.
- The anthropogenic signal in the ocean is only
a few
percent of the (unknown) natural background of dissolved inorganic
carbon (DIC).
- Carbon in the ocean participates in rather complex in
situ
biogeochemistry.
- Due to long transport time scales, the Cant
distribution in the
ocean is highly heterogeneous.
Thus, unlike the
atmosphere, which is relatively well
mixed, and
where we have ice core and instrumental data going back many thousands
of years, the ocean is much more challenging in this regard. What we do
know about Cant in the ocean is based on so-called "back
calculation"
methods that attempt to separate the small anthropogenic perturbation
from
the large background. The essential idea, which goes back to work by
Brewer, Chen, and Millero, is that we can estimate Cant by
correcting the measured total inorganic carbon for changes due to
biological activity. The basic equation is shown below,
where the first term is the measured DIC, the second is the change in
DIC due to soft tissue remineralization and carbonate dissolution, and
the third term is the air-sea CO2 disequilibrium when the
water sample was
last in contact with the surface.
Cant
=
DICmeas - biological correction - air-sea
disequilibrium correction …
Estimating these terms is a
messy business to say the
least, and it
requires making several critical assumptions:
- The stoichiometric or so-called Redfield ratios
necessary to
account for the biology are known and constant,
- Mixing in the ocean is a negligible component of
tracer transport
compared with advection (the so-called "weak mixing" assumption), and
- The air-sea disequilibrium has remained constant over
the
industrial era.
How valid are these
assumptions? As we see below, not
very. However, before we get to that, its useful to see what sort of
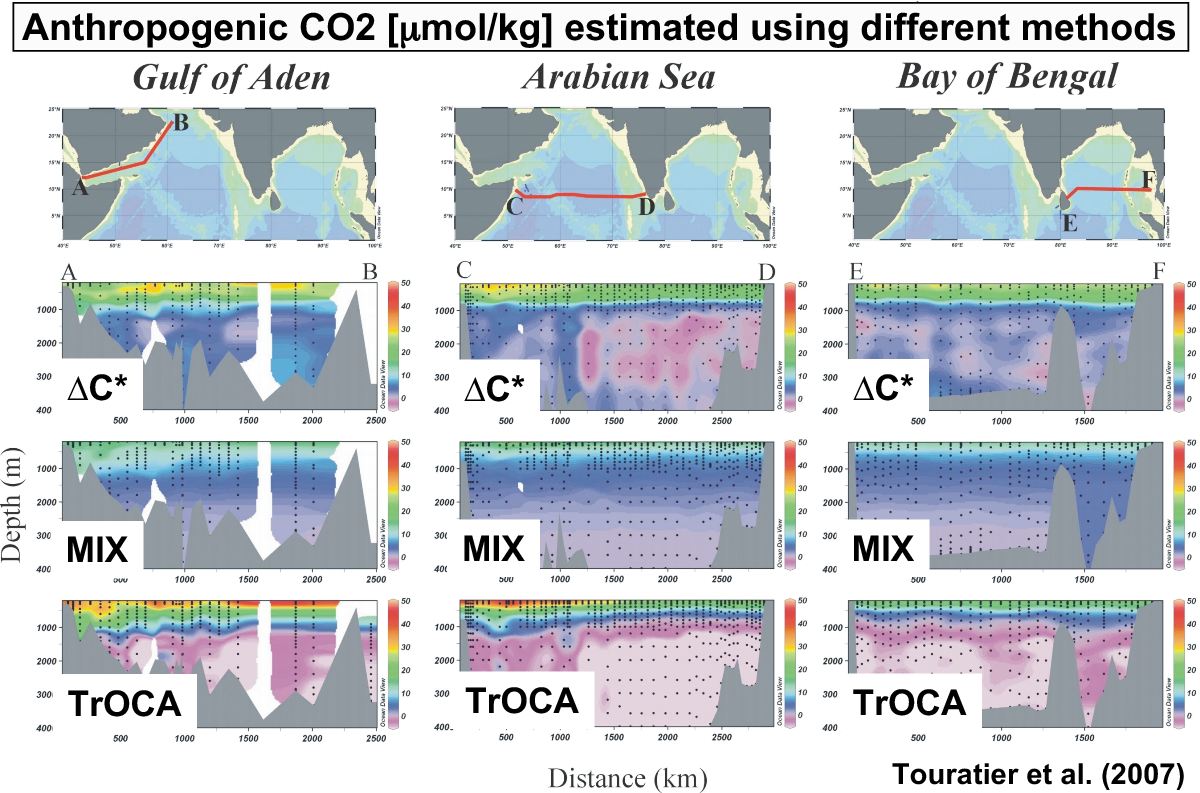
results can be obtained with traditional inference methods. The figure
below compare the
results of applying three different back calculation methods to
estimate anthropogenic carbon in the Indian Ocean. Clearly, while there
is some qualitative agreement between them, there are large
quantitative differences as well. In fact, integrated inventories
differ on average by 20% between the different methods. And many of
these methods, including the "ΔC*" method, which is perhaps the best
known of all, give negative
values of anthropogenic carbon, which points to serious problems.
Lastly, back calculation methods can only provide us with a single snapshot in time.
Considering that only one attempt has been made thus far to apply the
ΔC* method globally (Sabine et
al., 2004), resulting in an estimate for the mid-1990's, this is a
perhaps one of the major limitations of this approach.
Assumption I: Redfield ratios are known and constant in
space and time
A key assumption made by
back calculation methods is that we know what
Redfield ratios to use to correct for the biology. The difficulty with
this is that there are in fact large uncertainties in our knowledge of
the Redfield ratios and this translates into a correspondingly large
error in the inferred Cant. As an example, the plot below,
from
Wanninkhof et al. (1999), shows the fractional uncertainty in the
inferred Cant using the ΔC* method by propagating a
typical (12%) uncertainty in the C:O remineralization ratio. The error
is not
small even for large values of Cant. In the upper ocean,
this can
easily translate into a 30-50% uncertainty in the inferred Cant.
Assumption II: Ocean transport is dominated by
advection
A second implicit but
crucial assumption is that ocean
transport is
largely advective in nature. This is an implicit assumption because
back calculation techniques use transient tracers (which have a
time-varying input into the atmosphere and hence the surface mixed
layer of the ocean) such as CFCs to infer
the time it takes for a fluid parcel to go from the surface to the
interior. This works as follows. If you assume there is no mixing, then
the measured interior tracer concentration is related to the surface
history of the tracer through a simple time lag. If you know the
surface history you can calculate the time lag. This is shown
schematically in the figure on the left below.
Mathematically, we can write this as:

However, even though it
underlies much of chemical
oceanography,
this simple picture of the ocean is fundamentally incorrect. The ocean
is turbulent and diffusive, and in the presence of mixing there is no
unique time scale or pathway that connects the ocean surface to an
interior point. Instead, there is a multiplicity of pathways and
associated transit times (see schematic on right, above), that is, a
probability distribution of transit times or "transit time
distribution" (TTD). Consequently, the measured tracer concentration is
a weighted average of the surface history of the tracer, the
appropriate weight being given by a TTD or, more generally, a Green
function G, and expressed
mathematically
as a convolution integral:

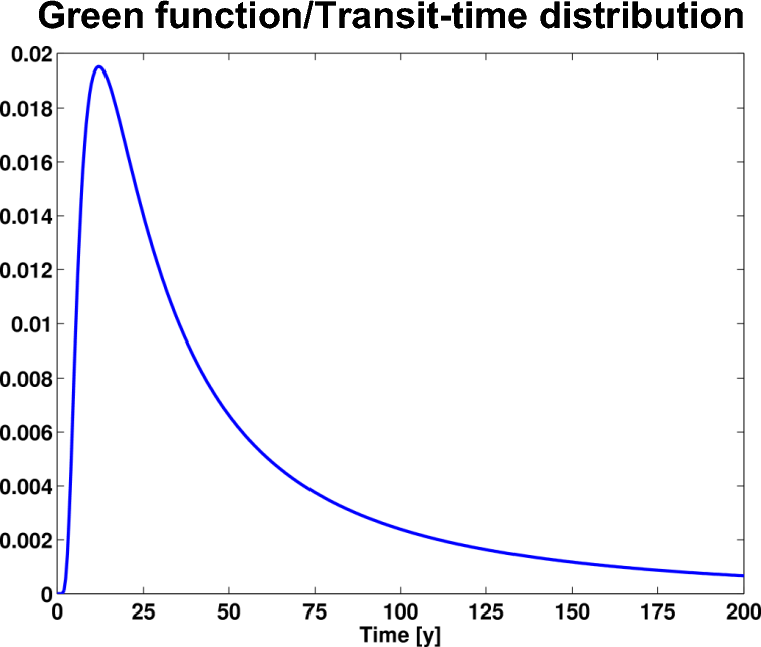
You can
think of G
as a
way to partition each water parcel according to when and where it was
last in contact with the surface. A typical example of a TTD
or G is shown below. Note in
particular the early peak and long tail that seems characteristic of
advective-diffusive transport in the ocean. Also note that the Green
function for purely advective transport would be a delta function
centered at the appropriate "transit time".
There is plenty of
evidence for this messier view of the ocean. As an
example, the figure on the left below shows the observed relationship
between two different tracers (CFC-11 and CFC-12) in the Indian Ocean.
The gray dots represent data while the various curves are attempts at
modeling the observed tracer distributions with TTDs (or G's) of different
widths. Evidently, the data are best explained by broad G's implying
strong mixing. The purely advective case (red line) is completely
inconsistent
with the data, something we find in other ocean basins as well.
The plot on the right
shows simulations in a 1º resolution data-assimilated
ocean general circulation model. (The simulations were performed
using the
Transport
Matrix Method (TMM) developed by us, an efficient new
technique for performing biogeochemical tracer simulations.) Here too,
we see broad TTDs, a feature that seems independent of model resolution.
Effect of mixing on Cant
So how does the neglect
of mixing impact estimates of anthropogenic
carbon? The figure below shows the inferred Cant as a
function of
measured
CFC-12 concentration for two scenarios. The first, shown in blue,
assumes perfect advection. The second, shown in red, assumes strong
mixing. You can see that in the upper ocean (higher CFC concentrations)
the difference between the two is small, i.e., CFC is a good proxy for Cant.
But at intermediate depths the no-mixing assumption predicts
substantially higher values of Cant. This is because the
no-mixing
estimate is based on tracer ages which are biased toward younger
values. Since anthropogenic carbon in the surface ocean is increasing
over time, this results in a higher estimate of anthropogenic carbon in
the interior. In the deep ocean, the bias is the opposite. If there is
no detectable CFC, we assume that there is no anthropogenic carbon,
which really cannot be true in the presence of finite mixing and the
fact that anthropogenic carbon has been around for a lot longer than
CFCs. Hence, this leads to an underestimate.
Assumption III: Constant air-sea disequilibrium
The third assumption is
that the ocean surface has kept up with
increasing levels of atmospheric CO2. This is known as the
constant
disequilibrium assumption. Now, there are two main reasons why the
ocean is not in equilibrium with the atmosphere. The first
is the fact that it takes a finite amount of time for air-sea exchange
of gases. This is about a month for most gases, but for CO2
it is about a
year because of its buffer chemistry in seawater. The second reason is
ocean circulation which is continuously pumping CO2-depleted
waters away from the surface at high latitude and bringing up CO2
enriched water in the tropics. This is why the subpolar ocean surface
is highly undersaturated while the tropics are oversaturated. The
assumption is that this air-sea disequilibrium has remained unchanged
over the industrial period. To
evaluate how well this assumption holds, we have performed explicit
simulations of anthropogenic carbon in an ocean biogeochemical model.
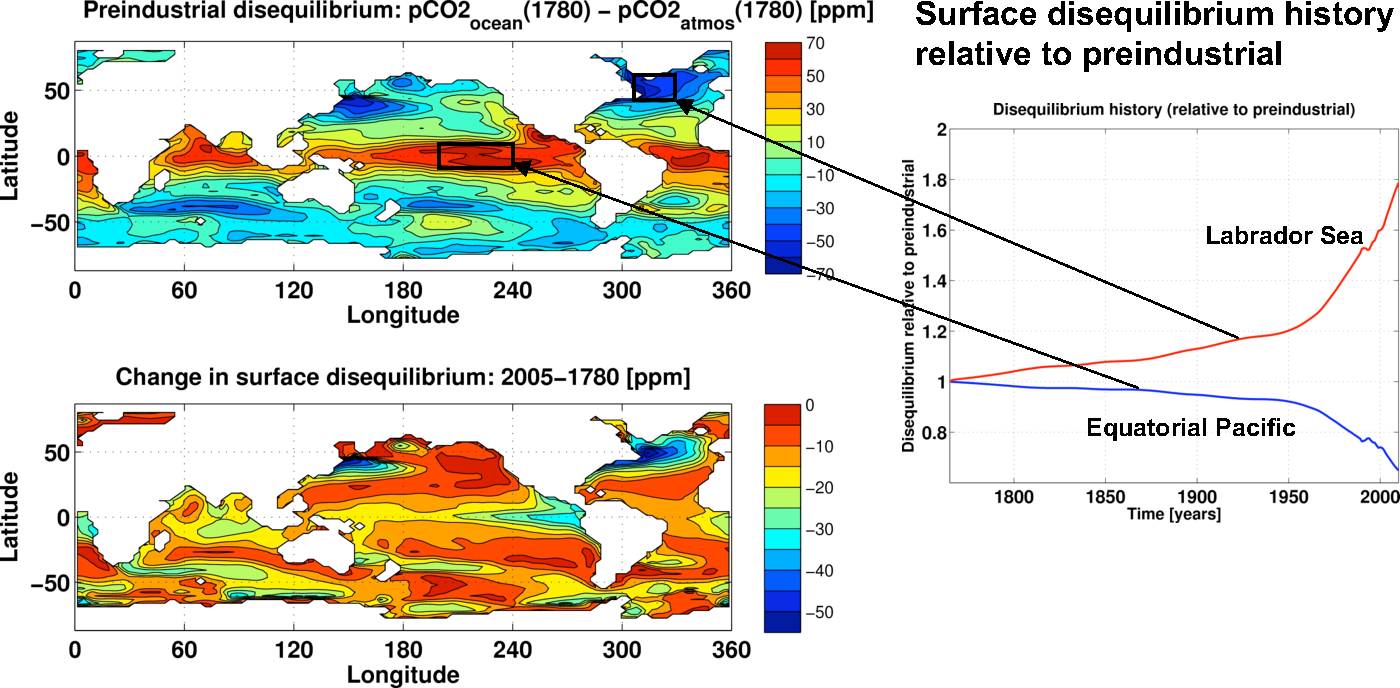
The top right panel in the figure below shows the preindustrial
disequilibrium (surface ocean pCO2
minus atmospheric pCO2)
in the
model. The bottom panel shows the change
in disequilibrium between the preindustrial and 2005. It is evident
that the changes are quite substantial. In fact, in the Labrador Sea
the disequilibrium changes by ~80%, while in the tropical pacific it
changes by ~40%. Since much of the anthropogenic carbon enters the
ocean at high latitude regions such as the Labrador sea, the constant
disequilibrium assumption leads to an overestimate (by almost 20%) in
the estimated anthropogenic CO2. More fundamentally, as we
show below, the uptake of anthropogenic CO2 by the ocean is
in fact driven by the change
in disequilibrium. Thus, assuming constant disequilibrium to estimate Cant
uptake is a contradiction.
Estimates of Cant based on ocean models
The discussion above has
focused on observational-based methods for estimating Cant
in the
ocean. A much simpler approach is to directly simulate anthropogenic CO2
in coupled carbon cycle-ocean circulation models, an approach taken
by a number of recent studies (e.g., Mikaloff-Fletcher et al., 2006).
The problem with this approach, however, is that there is little
agreement between different ocean models because they often have rather
different physical circulations. In fact, as seen in the figure below,
out of 19 models participating in the OCMIP-2 study (Matsumoto et al.,
2003), only two managed to simulate both the Southern Ocean CFC-11 and
anthropogenic CO2 inventories within the estimated error.
Certainly,
over time ocean models will improve and will be essential for
predicting future ocean CO2
uptake.
But first
they will need to be evaluated against data-based estimates of Cant,
which as the discussion above shows remain highly problematic and
limited.

A New Approach to Estimating Cant
To overcome the problems
and limitations of traditional methods for
estimating anthropogenic CO2 in the ocean, we have developed
an
alternative approach. In many
ways it is a much simpler and cleaner approach than back calculation
methods because it makes no attempt to separate the
small anthropogenic component from the large background. Our method
not
only
allows us to relax many of the (incorrect) assumptions traditionally
made, it
also uniquely provides us with the time-evolving spatial distribution
of
anthropogenic carbon over the entire industrial era. The basic
ideas and assumptions are as follows:
- The anthropogenic perturbation is sufficiently small
for us to
treat Cant as a conservative tracer that is
transported by the circulation from the surface to the interior.
- Ocean transport can be characterized by a Green
function.
- Ocean circulation is in steady state.
Given these assumptions,
we
can write the interior anthropogenic carbon concentration as a
convolution of the
surface history of Cant with the Green function G:
The time integral above
is over the industrial era and the space integral is over the ocean
surface (since different regions will in general have different surface
histories). To apply this equation, we need two pieces of
information: The Green function G,
and the surface history of
anthropogenic carbon.
Estimating G
from tracer observations
Since the Green function G
is an intrinsic property of the ocean
circulation, and not of any particular tracer, the concentration of any
passive
conservative tracer satisfies an equation analogous to that for Cant:
We exploit this fact by
using a suite of well sampled oceanic tracers such as CFCs,
temperature, salinity, radiocarbon, and nutrients, to deconvolve the
above equation for G. To
regularize this under-determined problem we use a maximum
entropy (ME) method. In practice, to reduce the indeterminancy, we
assume that the ocean circulation is in steady state except for a
cyclo-stationary seasonal cycle and we discretize the sea surface
position variable, x', into a
discrete set of surface patches. The ME solution for the i-th patch is
then given by:
where M is a prior estimate of G,
and αj is the Lagrange
multiplier required to enforce the j-th
observational
constraint. Substituting the above solution into the
convolution
integral for each tracer results in a small nonlinear problem whose
solution is the α's.
The figure belows shows a
particularly successful example of the
inversion. The blue line shows the directly simulated G in an ocean
model. Several tracers were also simulated in the same model and the
ME method was applied to these synthetic data. The red line shows
the
resulting ME inverse solution. The prior estimate used is
shown by the green line. Here, for illustrative purposes we have used a
uniform prior. In practice, we use analytical solutions to the 1-d
advection-diffusion equation as priors.
Estimating the surface history of Cant
The second piece of information we need is the surface history of C
ant.
To
estimate this boundary condition, we enforce mass conservation, i.e.,
require that the rate of change of the inventory of C
ant in
the ocean
be equal to its net flux into the ocean:
The air-sea flux of C
ant is in turn given by:
where k is a gas-transfer coefficient, D represents the air-sea
difference, and d represents
the anthropogenic
perturbation. This equation shows that the flux is proportional to the change in surface
disequilibrium of CO2. To make further
progress, we
exploit the
empirical result from ocean carbon cycle models (shown below from one
such model)
that the change in disequilibrium is to a very good
approximation, proportional to the (known) anthropogenic perturbation
in atmospheric pCO2:
where
e is the (unknown)
proportionality constant.
Combining the above equations with the equilibrium chemistry for CO
2
in
sea water, and requiring that our solution match observed
pCO
2 values
averaged over a discrete set of surface patches allows us to rewrite
the mass conservation equation entirely in terms of
e. Discretizing this equation in
time and space then results in a nonlinear equation for the discrete
set of
ei (one for each surface patch
i). We solve it using
least-squares.
To summarize, then, our inversion method provides improvements to
reduce the main biases of most previous techniques. In particular,
- The air-sea disequilibrium is allowed to evolve in
space and time.
- No assumptions are made on biogeochemical processes
or parameters such as Redfield ratios.
- The mixing of waters of different ages and end-member
types is explicitly accounted via a Green function constrained using
multiple steady and transient tracers.
Verification of Green function method in an Ocean Model
As a first step, we have
applied our approach to synthetic
tracer
"observations" simulated in a global ocean model. Tracers simulated
include, CFCs, natural 14C, nutrients, and O2.
As
"truth", we also simulate anthropogenic carbon.
The figure below shows
the column inventory of Cant
simulated in the
model (left) and the error between the ME inverse solution and the
"true" simulated solution. The agreement between the
two is remarkably good, with maximum
differences of O(2 mol/m2) in the Southern Ocean. The total
inventory simulated in 1995 in the model is 123.7 PgC, while the
inverse method gives an inventory of 125.9 PgC, an error of less than
2%.
Reconstruction of Anthropogenic CO2 in the
Ocean
Having gained confidence
in our method from the synthetic
inversion, we next applied it to oceanographic data. Tracers used
include gridded fields
of CFC-11, CFC-12, and natural 14C from the GLODAP database
(Key et al., 2004), and temperature, salinity, oxygen and phosphate
from the World Ocean Atlas (2005). Following Broecker et al. (1998),
oxygen and phosphate are combined into a quasi-conservative tracer
known as PO*. The
surface is partitioned into 26 discrete patches based on sea water
density. pCO2 data
required to estimate the Cant surface boundary condition are
taken from the Takahashi et al. (2009) database. Using
our new inverse method on this suite of observations, we have
reconstructed the first 3-dimensional, time-varying, history of
anthropogenic carbon in the ocean from 1765 to 2008.
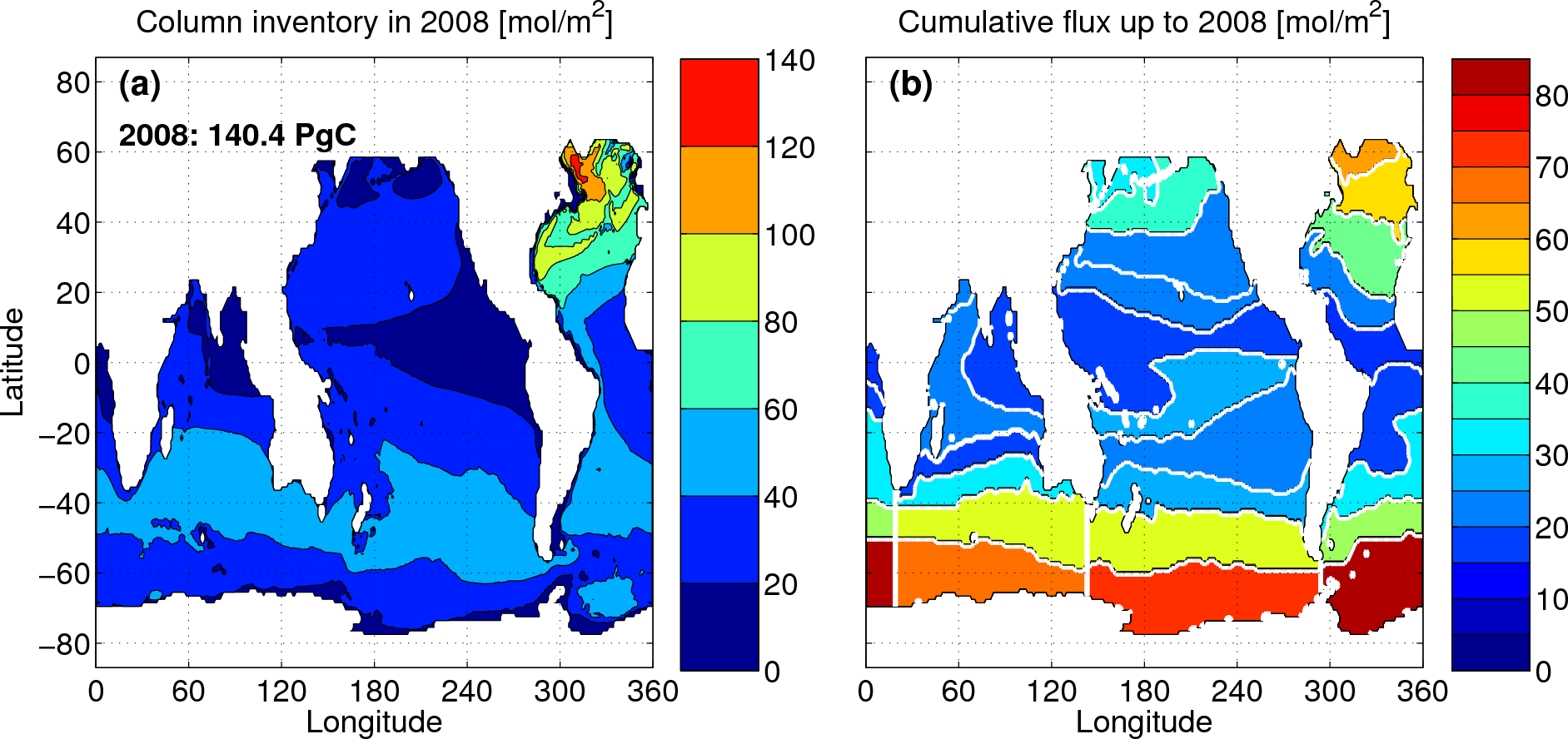
The figure on the left below shows the column inventory of Cant
in
2008. The total inventory in that year was ≈140±25 PgC. (The Arctic
Ocean and marginal seas are not covered by the GLODAP database. Using
the recent estimate of Tanhua et al. (2009) for the former, and the
area scaling approach advocated by Sabine et al. (2004) for the latter,
would increase our estimate of the global
inventory by ~11 PgC.)
The animation below shows the column inventory of anthropogenic carbon
over the industrial period. The movie runs from 1775 to 2007. The total
inventory is shown in the upper left corner.
These are net global
estimates, but, uniquely, we can go further. We can
partition the uptake according to where at the surface the
anthropogenic CO2 penetrated the ocean. As is evident from
the right panel in the figure above, the high latitude oceans, driven
by intermediate and
deep water formation, constitute the most intense sinks of Cant.
(The white lines in the figure delineate the 26 surface patches used
for the inversion.) In
particular, the Southern Ocean is by far the largest conduit by which
anthropogenic CO2 enters the ocean: roughly 40% of the Cant
residing
in the ocean in 2008 entered the ocean south of 40ºS. Interestingly,
only a small fraction of the CO2 taken up by the Southern
Ocean accumulates in that region. Much of this CO2 is
transported northward by ocean circulation. The animation below shows
the cumulative uptake (in PgC)
through each of the 26
surface patches. The movie runs from 1775 to
2007.
It is useful to compare
our results with previous estimates of Cant in the ocean. To
date, only
two global estimates of Cant have been made. Both are
snapshots for
1994. Our estimate of the global inventory in that year is 114±22 PgC,
which is consistent with both the ΔC* based estimate of 106±21 PgC
(Sabine et al., 2004), and the TTD-derived estimate of 107 (94-121) PgC
(Waugh et al., 2006). However, the previous TTD based estimate
incorrectly treated air-sea disequilibrium as constant. To account for
this, Waugh et al. included an ad-hoc 20% downward correction based on
numerical model simulations in their reported result. Our estimate does
not require such a correction because our inverse method explicitly
accounts for changing air-sea disequilibrium. While our estimate for
the global inventory also agrees well with the ΔC* based estimate, the
spatial distribution we obtain is quite different. In particular,
relative to the ΔC* based estimate, our estimate of Cant is
generally
lower in the upper ocean and higher in the deep ocean. The reasons for
this can be understood in terms of the various assumptions made by the
ΔC* method. In particular, two
fundamental assumptions of the ΔC* are the use of a single tracer age
to characterize transport (effectively assuming that ocean circulation
is essentially advective) and that air-sea disequilibrium has remained
constant since the start of the industrial period. As the discussion
above showed, both these assumptions are incorrect, and give rise to
competing biases which happen to largely cancel out, leading to the
close, but fortuitous, agreement in total inventory estimated using the
ΔC* method and our estimate.
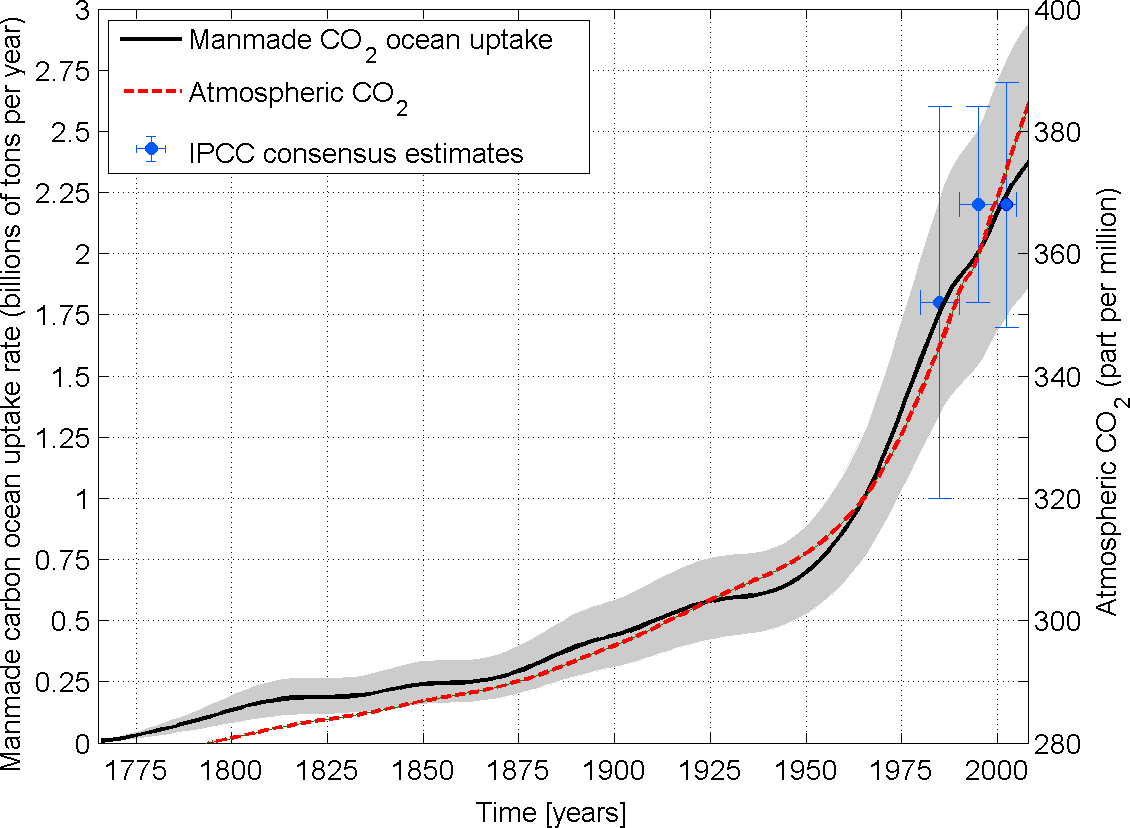
So much for the inventory
and distribution of Cant. What about the uptake rate? From
the
time-varying inventory, we can compute the uptake history over the
industrial era. The figure below shows the uptake between 1765 and
2008. As is evident, the uptake rate has changed dramatically over
time. In particular, there was a sharp increase in ocean uptake since
the 1950's, driven by the higher growth rate of atmospheric CO2.
It currently stands at 2.3 PgC/y, i.e., for every four tons of CO2
that humans produce, the oceans absorb a bit over a ton.
More
recently, however, while the uptake rate has kept on increasing, its
rate of increase
appears to have slowed somewhat even though
atmospheric CO
2 levels continue to increase at roughly the
same rate.
This seems consistent with recent evidence (
Canadell et al., 2007) for an increase
in
the airborne fraction (the proportion of human CO
2 emissions
that remain in the atmosphere), suggesting that the intensity of both
the land biosphere and ocean sinks is declining. Indeed, we find that
between 2000 and 2007, the fraction of emissions taken up by the ocean
has declined by almost 10%. Why might this be? Since we assume a steady
circulation, it can't be
due to changes in
ocean circulation as suggested by some recent studies based on ocean
climate models. For example,
Le
Quere
et al. (2007) claim that the Southern Ocean sink of manmade carbon
is declining - in the model - because of an increase in the strength of
the meridional overturning circulation in response to changes in the
westerly winds. This is debatable, however, since there are both
empirical and theoretical grounds for suspecting that coarse resolution
ocean models - in which eddies are parameterized - do not correctly
capture the behavior of the real ocean. We should also keep in mind
that the rate of growth of emissions is increasing. According to
Raupach et al.
(2007), the growth rate of emissions has increased sharply this
decade compared with the previous one. Between 1990-1999 emissions grew
by 1.1% per year, while from 2000-2004 they grew by over 3% a year,
almost a 3-fold increase. Taking these together, there are two
plausible explanations for why the ocean uptake is slowing down
relative to emissions. The first explanation is ocean chemistry. As
the ocean takes up CO
2,
its
capacity to take up more anthropogenic carbon decreases due to the
nonlinear nature of the CO
2 chemistry in sea water. This
"buffering" effect is well understood. In fact,
when we
linearize the chemistry in our calculations, the aforementioned decline
in
the rate of increase of uptake reduces substantially. The second
explanation is that the ocean is simply not able to 'keep up' with the
rapid growth in emissions. There is a physical limit (due to air-sea
gas exchange and ocean circulation) on how rapidly CO
2 can
enter the ocean. If the emissions grow too quickly, then the ocean
can't keep up. Indeed, we have
shown
recently that the airborne fraction is quite sensitive to the emission
history and that a 10% increase in the rate-of-growth of emissions
leads to a 3-4% increase in the airborne fraction. Thus, rather than
invoking 'exotic' mechanisms such as large scale changes in ocean
circulation, we believe it is basic physical and chemical factors that
are limiting the ocean's ability to take up fossil fuel CO
2.
Also shown on the figure above are
the IPCC AR4 "consensus" estimates. (These are decadal averages.) There
is generally
good agreement between our estimates (which cover the entire industrial
period) with the IPCC ones (which only go back to the 1980's). In
particular, our estimate for the present decade is 2.3±0.6 PgC/y, while
the IPCC estimate (which is actually based on an ocean model) is
2.2±0.4 PgC/y.
Implications for the Role of the Terrestrial Biosphere
in Uptake of
Anthropogenic CO2
One of the major uncertainties in our understanding of the
anthropogenically-perturbed carbon cycle is the role of the terrestrial
biosphere. Since direct CO
2 flux measurements, especially on
a global
scale, are at best difficult to make, the terrestrial source/sink term
has typically been computed as a difference between the relatively well
constrained source of anthropogenic CO
2 due to fossil fuel
burning, and
the atmospheric and ocean sinks. The difficulty with this approach is
that until now only a single estimate of the inventory of C
ant
in the
ocean has been available (for 1994). To get around this, scientists
have resorted to using numerical models of ocean CO
2 uptake
to quantify
the land term. However, as discussed above, this approach has its own
problems, among them being the large errors in simulated transport in
current ocean models, and the correspondingly large disagreement in
simulated uptake between different models. Our time-evolving, purely
data-based estimate of the ocean
uptake allows us to circumvent these problems, and provide a more
precise and detailed view of the land sink.
The figure below between shows the time evolution of the main fossil
fuel source and the ocean and atmosphere sinks between 1765 and 2005.
Also shown is the terrestrial biosphere inventory, computed as the
difference between the fossil fuel source and the ocean and atmosphere.
Sources are shown as positive values and sinks as negative values.
Fossil fuel data are taken from Marland et
al. (2007). As is evident, the terrestrial biosphere was a source of
anthropogenic carbon until the 1940's, subsequently turning into a
sink. Cumulatively over the entire industrial period, our best estimate
is that the terrestrial biosphere was a net source of C
ant.
Propagating
uncertainties, we find that the terrestrial biosphere has been anywhere
from neutral to a net source of CO
2, contributing up to half
as much C
ant as has been taken up by the ocean over the same
period.
In the discussion above,
we only included fossil fuel burning as a source of anthropogenic CO2
in the computation of the "net terrestrial sink". However, another
source of Cant is changes in land use, estimates of which,
as mentioned previously, remain highly uncertain. Including this term
as a source
provides a different perspective on the role of the terrestrial
biosphere. The figure below show the evolution of what is sometimes
termed the "residual terrestrial sink" (computed as above, but
including land use changes (from Houghton, 2008) as a source). Note the
very large error envelope associated with this curve. Our best estimate
suggests that cumulatively, the terrestrial biosphere
currently contains roughly the same amount of anthropogenic CO2
as the ocean. However, given the uncertainty, the terrestrial biosphere
could be anywhere from neutral to twice as important a sink of
anthropogenic CO2 as the ocean.

Implications for Future CO2 Uptake and Ocean
Chemistry
Lastly, we explore the
implications of our work for future CO2 uptake by the ocean.
As discussed above, our results suggest that changes in ocean chemistry
(i.e., acidification) may already be limiting the ability of the ocean
to take up more manmade CO2. It is therefore useful to
explore how continued penetration of CO2 by the ocean will
impact ocean chemistry and thus the role of the ocean as a sink of man
made CO2. As a preliminary step, we have used our Green
function method to predict future CO2
uptake in response to projections of atmospheric CO2.
As an example, the animation below shows the evolution of
the
aragonite
lysocline depth for 4 different IPCC emission scenarios, starting with
the most aggressive (A1FI) in the top left corner to the least
aggressive
(B2) in the bottom right. The movie runs from 2000 to 2100. The
lysocline represents the surface above which CaCO3 is able
to
precipitate out of seawater (and form shells). Below this surface, the
water is undersaturated with respect to CaCO3. As is
evident, by the
year 2100, much of the surface Southern Ocean and large parts of the
North Pacific become undersaturated for the A1FI scenario (grey
shading). Even in the most optimistic case (B2), we find that many
parts of the
surface Southern Ocean become undersaturated.
Summary
We have developed a new, purely data-based, inverse method to
reconstruct the first 3-dimensional, time-varying, history of
anthropogenic carbon in the ocean over the industrial period
(1765-2008). Our approach overcomes many of the
fundamental problems
and limitations that have hindered previous attempts at solving this
problem, and provides the most
comprehensive view to date of the ocean sink of manmade carbon. We
find a total inventory of anthropogenic CO2 in the ocean in
2008 of ≈140±25 PgC (≈150 PgC if we include the Arctic), and a
corresponding uptake rate of 2.3±0.6 PgC/y.
Thus, the world's oceans currently absorbs roughly a quarter of
manmade carbon. Our reconstruction quantifies the spatial and temporal
distribution of
where at the surface this CO2 enters the ocean, and
indicates that roughly 40% of this CO2 penetrated via the
Southern Ocean. However, only a small fraction remains in the Southern
Ocean, with the bulk of it being transported northward by ocean
circulation. We also find that CO2 uptake has increased
sharply since the 1950's, with a small decline in the rate of increase
in the last few decades. In particular, between 2000 and 2007, the
proportion of emissions absorbed by the ocean has declined by as much
as 10%. There may be several reasons for this slowdown, but changes in
ocean chemistry, compounded by the ocean’s slow circulation in the face
of accelerating emissions, offer plausible explanations. This is in
contrast to other studies, based on climate models, suggesting large
scale changes in ocean circulation as a cause for the relative decline
in the ocean sink. Lastly, combining our reconstruction
with the known history of anthropogenic emissions, gives us a more
precise and detailed view of the terrestrial biosphere sink. Our
results suggest that the terrestrial biosphere was a source of CO2
until the 1940's, subsequently turning into a sink that has averaged
≈1.1 (0.4-1.8) PgC over the past decade. Cumulatively, the terrestrial
biosphere has been anywhere from neutral to a net source of CO2,
contributing up to half as much CO2 as has been taken up by
the ocean since the start of the industrial period.
Acknowledgment
This research was funded by the U.S. National Science Foundation.